

Polar codes are a recently discovered class of error correction codes that have been proven to achieve channel capacity at infinite lengths. They have also been shown to have excellent finite length performance in comparison with state-of-the-art LDPC and Turbo codes when used in conjuction with a CRC and list decoding. Polar codes have also been included in the upcoming 5th generation 3GPP standard for New Radio. As such, ISIP is committed to developing high quality polar code research that maximizes their utility for the future.
Fast simplified successive cancellation is what makes polar codes practical candidates for modern communication systems by significantly increasing the decoder throughput. The performance is achieved by realizing that a polar code can be broken down into constituent codes with fast optimal decoders. This improvement can be applied across the successive cancellation family of decoders: SC-List, SC-Flip, SC-Stack.
2012, A. Mishra, A. J. Raymond, L. G. Amaru, G. Sarkis, C. Leroux, P. Meinerzhagen, A. Burg, W. J. Gross

Semi-parallel architecture for the implementation of successive cancellation decoding.
Drastic reduction in processing complexity allows very large polar code decoders to be implemented in hardware.
An \(N=2^{17}\) polar code successive cancellation decoder is implemented in an FPGA. Synthesis results for ASIC are reported.
2014, Gabi Sarkis, Pascal Giard, Alexander Vardy, Claude Thibeault, Warren J. Gross
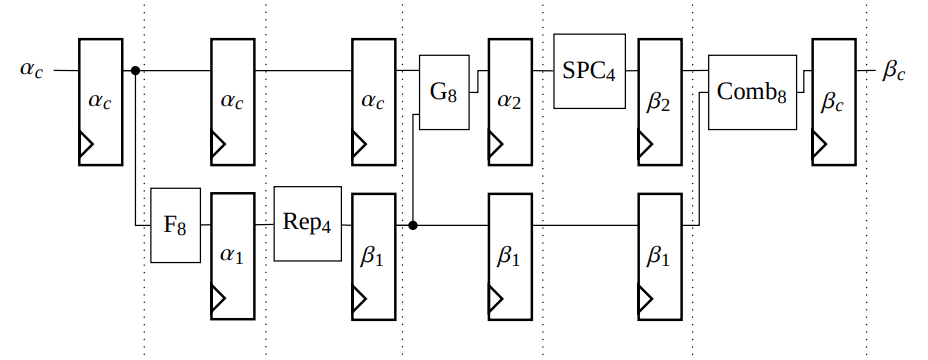
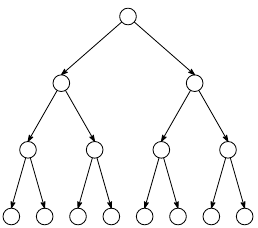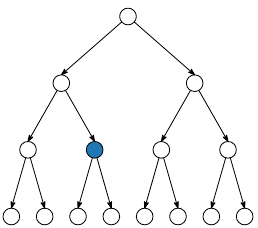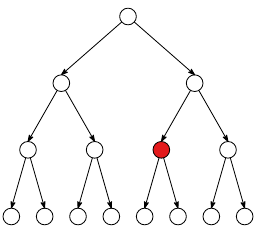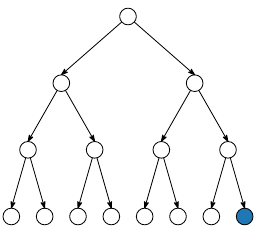
Identification of new special nodes, leading to: R0, R1, REP, SPC and combinations of themselves.
The decoding can be carried out in a more efficient way than fully exploring the decoding tree.
Optimal decoder: performs exactly as the original SC decoder.
Since the identified nodes can be decoded in parallel, Fast-SSC can decode a received vector with a much higher speed than SC. Typically, such an architecture can reach a T/P of 1 Gbps.
Even more, it is possible to generate a code-specific unrolled decoder. In that case, a hardware decoder can achieve a T/P faster than 200 Gbps.
2015, Ido Tal, Alexander Vardy
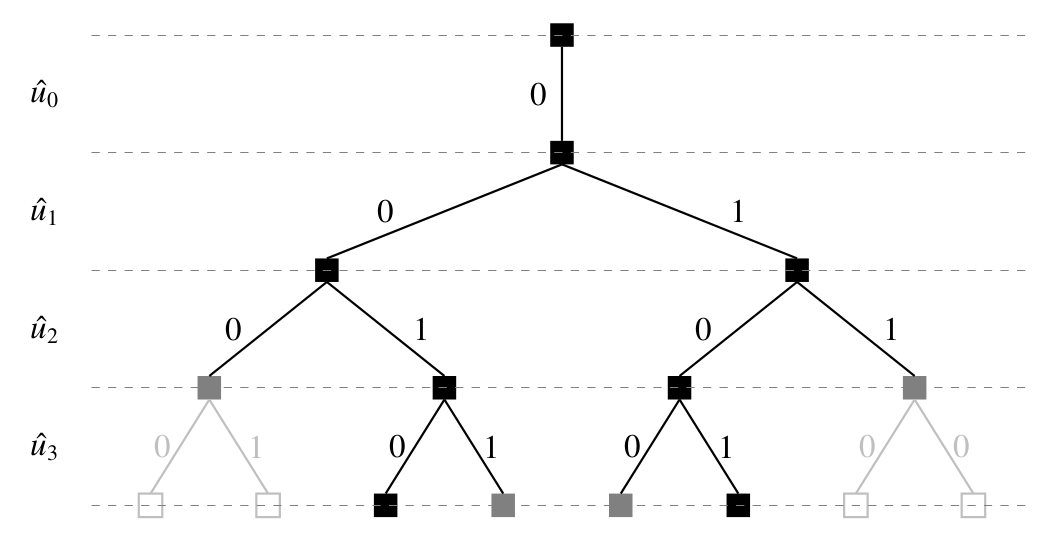
The SCL decoding algorithm estimates a bit with both possible values 0 and 1.
Each new bit estimate doubles the number of codeword candidates
To control the exponential increase in the complexity of this algorithm, only L codeword candidates are tracked.
Greatly improves decoding performance if an outer CRC code is concatenated with the polar code.
2017, S. A. Hashemi, C. Condo, W. J. Gross
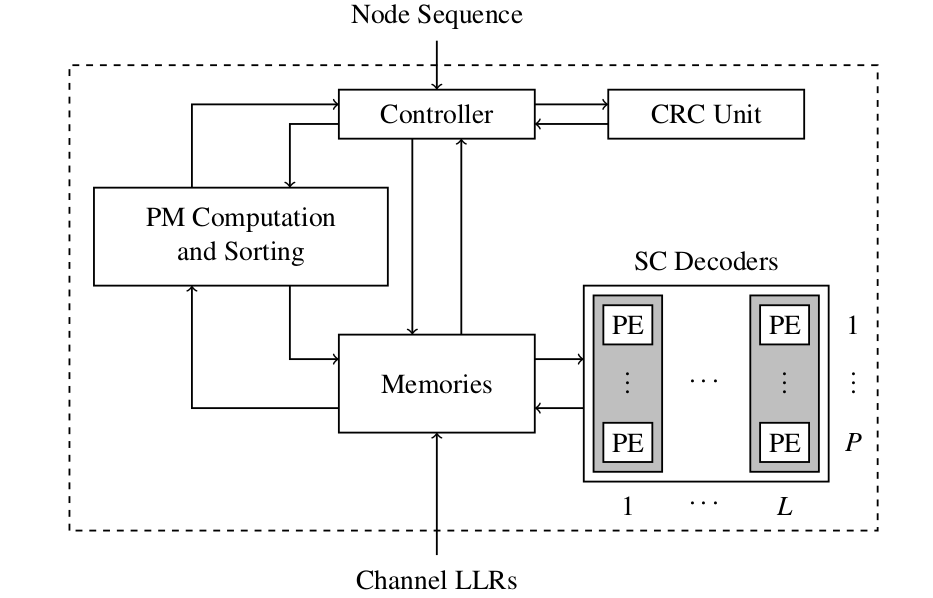
SCL decoding shows superior error-correction performance in comparison with SC decoding. However, this error-correction performance improvement comes at the cost of higher decoding latency and lower throughput.
Removing redundant calculations in the SCL decoding.
Optimization techniques which allow for negligible error-correction performance loss while providing a higher throughput and lower latency.
2018, S. A. Hashemi, M. Mondelli, S. H. Hassani, C. Condo, R. Urbanke, W. J. Gross
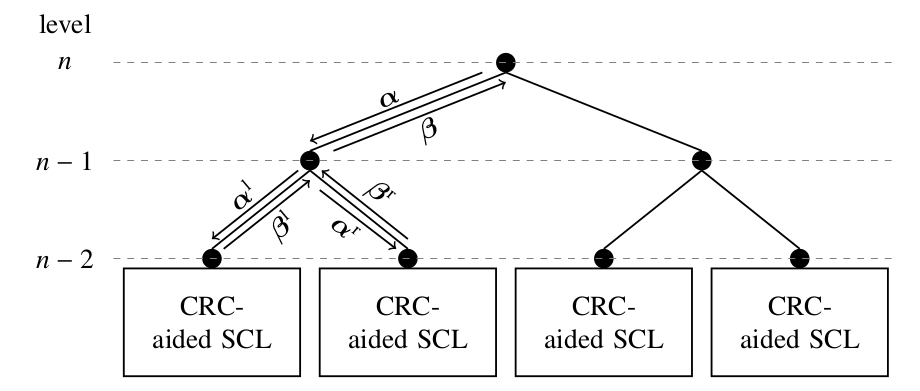
By performing SCL decoding on partitions of the decoder tree, memory can be shared between the different partitions of the code.
In the case of PSCL algorithms, only one path is transmitted across partitions. This algorithm can be extended to GPSCL and LPSCL, leading to a fine tuning of the trade-off between the error-correction performance and the decoder complexity.
2017, Frédéric Gabry, Valerio Bioglio, Ingmar Land, Jean-Claude Belfiore
2018, Gabriele Coppolino, Carlo Condo, Guido Masera, Warren J. Gross